ニューロンの活性化関数でよく使われるものにはいくつか種類がある。
まず、ステップ関数。
数式はこうなる。
$$f(x) = \left\{ \begin{array}{11} 1 & (x > 0) \\ 0 & (\mathrm{otherwise}) \end{array} \right.$$これはニューロンの概念を学ぶときに教科書上でよく使われる。後々取り上げることになるけれど、ディープラーニングの「学習」を行うときは活性化関数の「勾配」を使う必要があるから、このステップ関数のような勾配が無い関数は実用的ではなく、実際に使われることはない。
続いて、シグモイド関数。
形が少しステップ関数に似ているけれど、ちゃんと微分できるので一応使える。
数式はこうなる。
$$f(x)=\frac{1}{1+\mathrm{e}^{-x}}$$微分した式は次のように\(f(x)\)を使って簡潔に表現できるのが特徴。
$$f^{\prime}(x)\\ =\left(\frac{1}{1+\mathrm{e}^{-x}}\right)^{\prime}\\ =\frac{(1)^{\prime}\cdot(1+\mathrm{e}^{-x})-1\cdot(1+\mathrm{e}^{-x})^{\prime}}{(1+\mathrm{e}^{-x})^{2}}\\ =\frac{\mathrm{e}^{-x}}{(1+\mathrm{e}^{-x})^{2}}\\ =\frac{1+\mathrm{e}^{-x}-1}{1+\mathrm{e}^{-x}}\cdot\frac{1}{1+\mathrm{e}^{-x}}\\ =\left(1-\frac{1}{1+\mathrm{e}^{-x}}\right)\cdot\frac{1}{1+\mathrm{e}^{-x}}\\ =(1-f(x))f(x)$$最後に、ReLU関数。
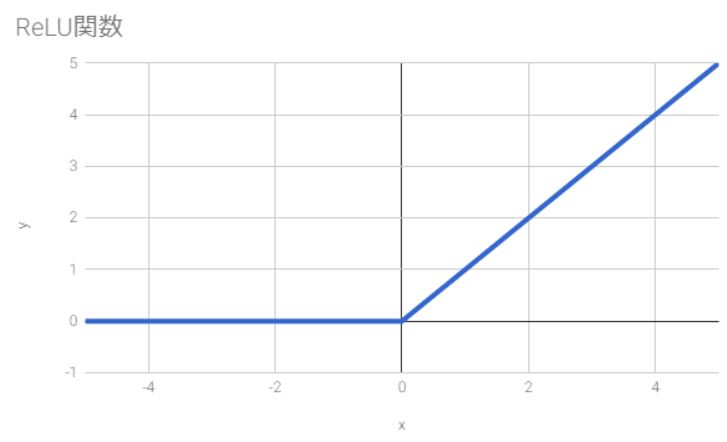
数式はこうなる。
$$f(x) = \left\{ \begin{array}{11} x & (x > 0) \\ 0 & (\mathrm{otherwise}) \end{array} \right.$$シグモイド関数でも一応は計算できるけれど、ニューラルネットワークの学習がなかなか思うように進まないことがしばしばあるので、現在ではこのReLU関数がよく使われる。これについて詳しくは後日。