もくじ
何が難しいのか
ボールは丸い。
丸いので,ボール同士が衝突して跳ね返る方向は単純な計算では求められない。
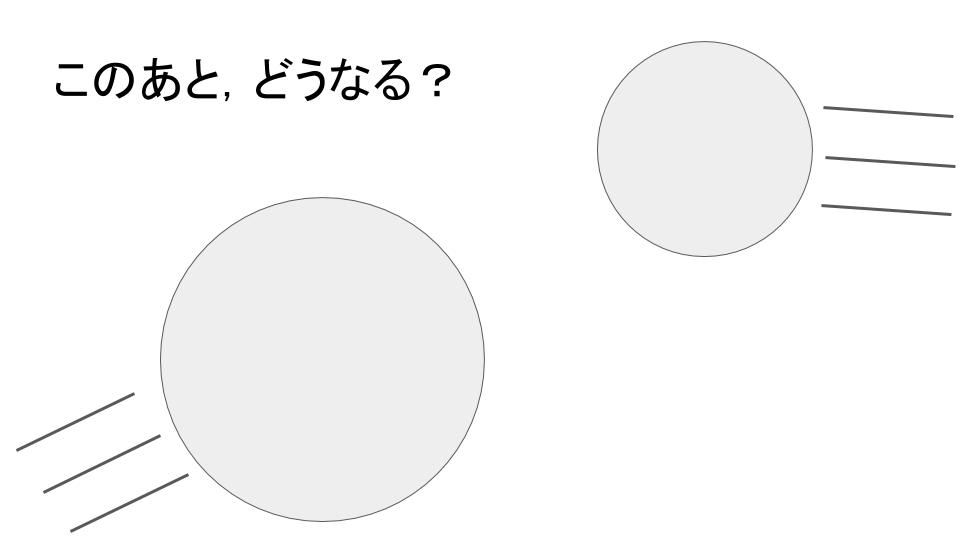
ボール同士が正面衝突したら,ボールはお互いに逆方向に跳ね返りそう,くらいの予想はできるけど,
かするように衝突したら?
大体こうなるのかな,というイメージはできても跳ね返る方向や跳ね返った後の速さは頭では正確にイメージできない。
ボールの重さが異なると問題はさらにややこしくなる。
ということで計算が必要だ。
計算の準備
問題の本質を考えるために次の仮定をしよう。
ボールはカッチカチのツルッツル! まわりは真空!

具体的には次のような表現になる。
- ボール自体は回転(自転)しない
- ボール表面の摩擦はゼロ
- ボール同士が衝突したときの反発係数は\(e\)
- 空気抵抗はゼロ
- ボールは剛体である(変形しない)
ここでは,ボールの衝突前後の状況を次のように表現する。
衝突前
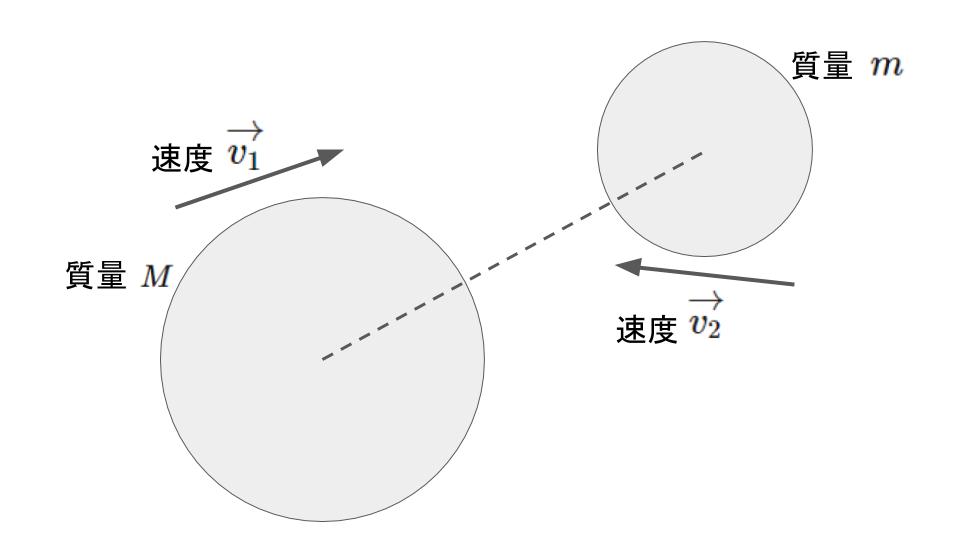
衝突後
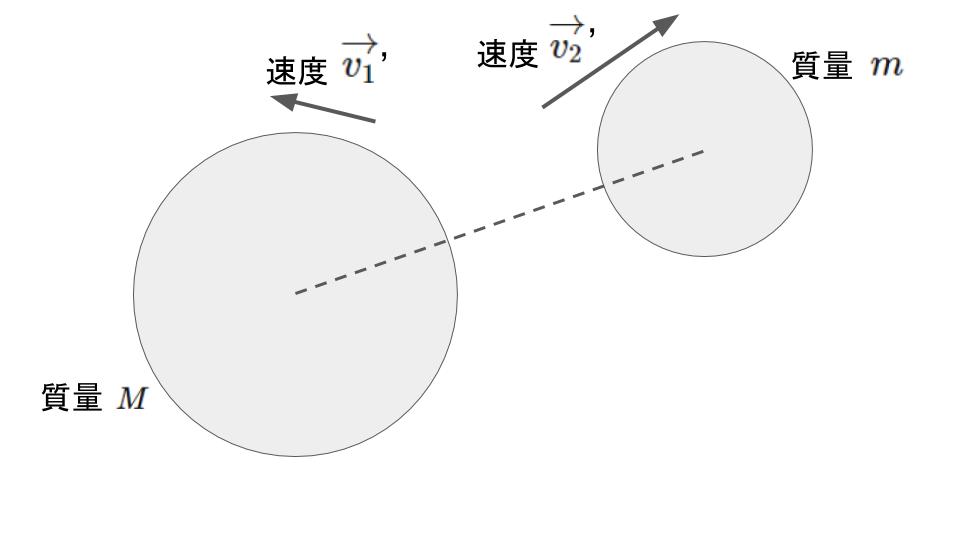
次の2つの成分に速度を分解して考える。
- 衝突する面に垂直な成分
- 衝突する面に水平な成分
今回ボール表面の摩擦はゼロであるため,「衝突する面に水平な成分」は衝突時に何ら影響を与えない。
従って,以降では水平な成分は無視し,垂直な成分のみ考慮する。
図に表すとこうなる。
衝突前
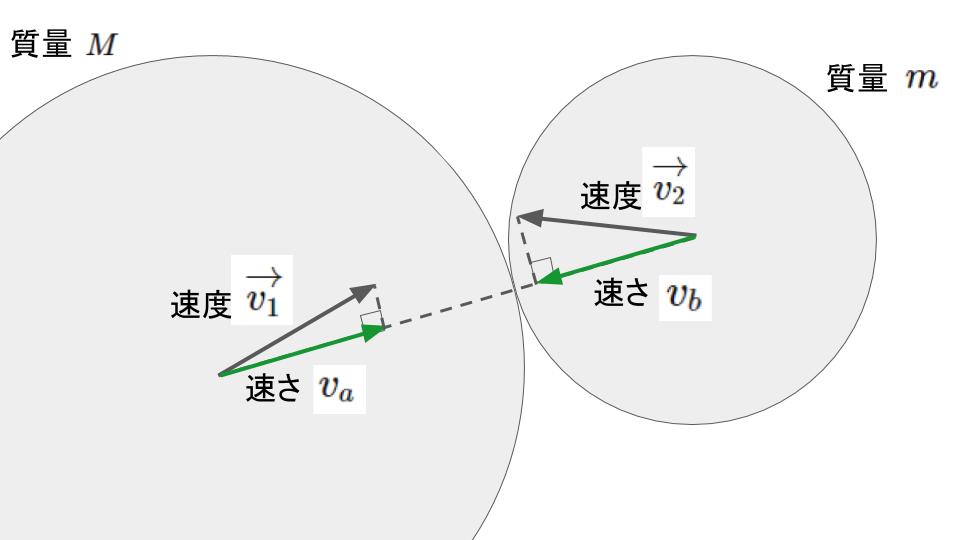
計算では速度\(\overrightarrow{v_{1}}, \overrightarrow{v_{2}}\)の内,衝突した面に垂直な成分\(v_{a}, v_{b}\)のみ使う。
衝突後
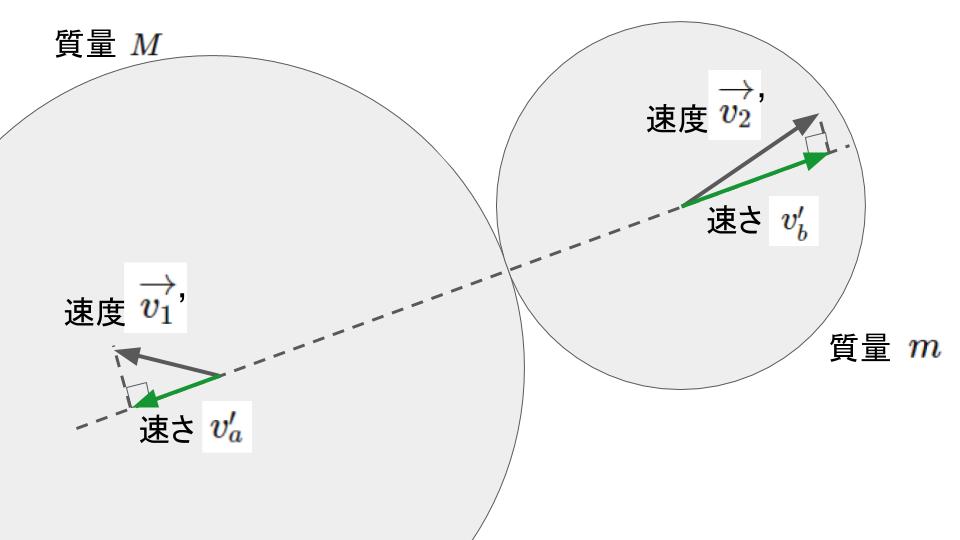
計算では速度\(\overrightarrow{v_{1}}^{\prime}, \overrightarrow{v_{2}}^{\prime}\)の内,衝突した面に垂直な成分\(v_{a}^{\prime}, v_{b}^{\prime}\)のみ使う。
反発係数
衝突の前後で,2つのボールの相対的な速度の関係は反発係数\(e\)を用いて次のように表現できる。
運動量の保存
衝突の前後で,2つのボールの運動量のうち,衝突する面に対して垂直な方向の成分の総和は変化しないので,次の式が成り立つ。
計算
以上から,次の連立方程式が得られた。
これを\(v_{a}^{\prime}\)と\(v_{a}^{\prime}\)について解くと,衝突後の速度の垂直成分が得られる。
結果だけ書くと次の通りとなる。
$$v_{a}^{\prime}=\displaystyle{\frac{Mv_{a}+mv_{b}-em\left(v_{a}-v_{b}\right)}{M+m}},\\v_{b}^{\prime}=\displaystyle{\frac{Mv_{a}+mv_{b}+eM\left(v_{a}-v_{b}\right)}{M+m}}$$
後は,速度\(\overrightarrow{v_{1}}\)の内,衝突面に垂直な成分\(v_{a}\)を\(v_{a}^{\prime}\)に上書きし,速度\(\overrightarrow{v_{2}}\)の内,衝突面に垂直な成分\(v_{b}\)を\(v_{b}^{\prime}\)に上書きすれば,求めたい速度\(\overrightarrow{v_{1}^{\prime}}\)と\(\overrightarrow{v_{2}^{\prime}}\)が得られる。
シミュレーション例
Processing3.5.3を用いてつくった簡単なシミュレーションの例。
つくったおもちゃ
ちょっとしたおもちゃつくってみた。
