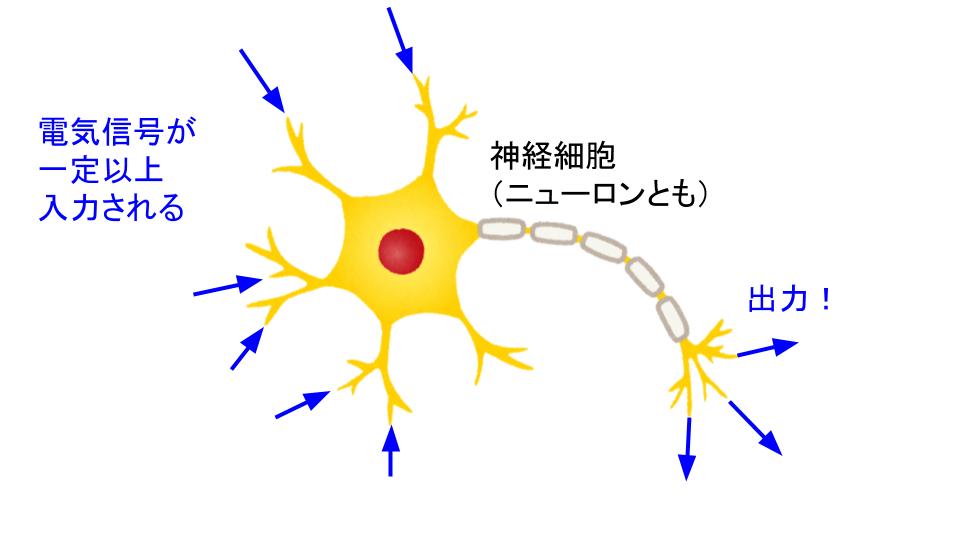
以前の記事で、脳がたくさんの神経細胞でできていて、ディープラーニングはその仕組をマネしたものだと説明した。
今回は、この神経細胞の電気的なはたらきをコンピュータ上で再現するための考え方を説明する。 前回のまとめになるけれど、神経細胞には次のような性質がある。
- 複数の入力がある。
- 神経細胞の出力は複数あるように見えるけれど、すべて同じタイミング・同じ強さで発生するので本質的に出力は1つ。
- 入力信号がある程度大きかったり、たくさん入力信号を受け取ったりすると、出力が発生する。
- 複数ある入力は、それぞれどれだけ出力を発生させやすいかが異なる。
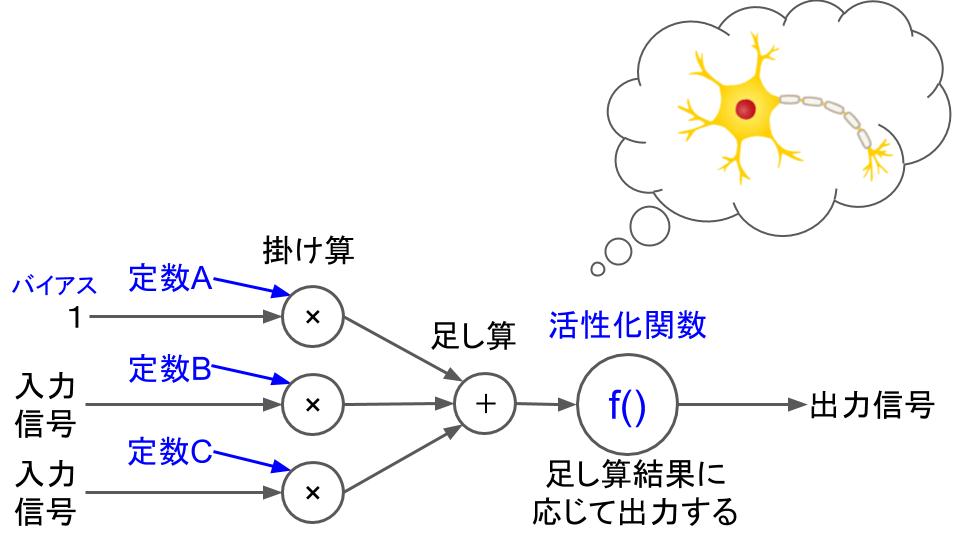
こうした特定の特徴だけをコンピュータなどに再現することを「モデル化する」という。 今回は神経細胞の性質の内、先程の電気的な性質だけをモデル化するので、細胞の重さや柔らかさなど他の性質は一切考慮しない。 結果からいうと、神経細胞をモデル化した結果は次の図のようになる。(結果は人によって違うと思うけど、これはディープラーニングでよく使われている例だ)
左から順に見ていこう。 まず、神経細胞に入力された電気信号には、それぞれ一定の数が掛け算される。 この一定の数は、上記の4の性質の「どれだけ出力を発生させやすいか」を表現しているので、神経細胞ごとに異なるし、1つの神経細胞の中でも入力ごとに異なる。 バイアスと書かれたものは、神経細胞の出力のし易さを調節するためのもので、常に1(最大)の信号が入力され、一定の数(図中の定数A)が掛け算される。この定数Aの値が大きいほど、神経細胞は出力し易くなる。 次に、すべての掛け算結果は足し算され、足し算結果は「活性化関数」への入力となる。 活性化関数については次回説明するけれど、今はステップ関数(入力が0未満で出力0、入力が0以上で出力1)のようなものと思ってもらってOK。こんなの↓
このような活性化関数の出力が、この神経細胞の出力になる。 活性化関数の形を見ると分かると思うけど、神経細胞の出力はディープラーニングの世界では基本的に0か1のどちらか(厳密には、0から1の間の小数)になる。 出力は、次の神経細胞の入力になり、その神経細胞の出力はそのまた次の神経細胞の入力に・・・という具合に、ニューラルネットワークはつくられる。 モデル化された神経細胞を論文や専門書などに図示するときは、次のように円と矢印で書くことが多い。