目次
多層パーセプトロンとは
パーセプトロン単体ではちょっと複雑な計算が行えないことは前の記事で説明している。
今回は、そうした計算の限界を克服するニューラルネットワークの構成の一つ「多層パーセプトロン」について説明する。
まず、多層パーセプトロンの最も単純なつくりはこんな感じ。
普通のパーセプトロンよりもニューロンの数が増えた。そして何やらニューロンが数珠つなぎになっている。
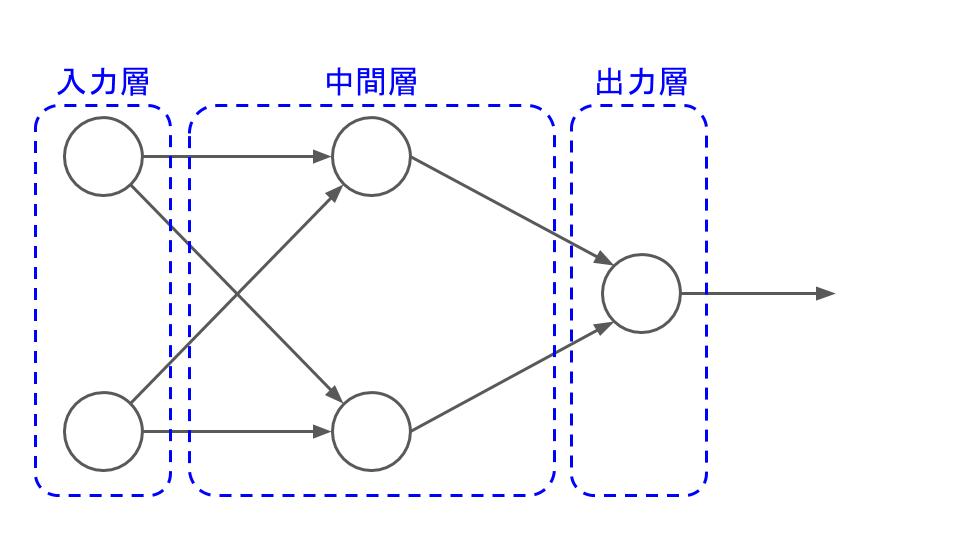
多層パーセプトロンは「層」という字に表れているように、ニューロンが層構造を成している。大まかには、次の図のように、入力層、中間層(隠れ層)、出力層の3種類。
多層パーセプトロンには次のような特徴がある。
- 中間層の層の数は用途に応じて人間が決める。
- 入力層、各中間層、出力層のニューロンの数は用途に応じて人間が決める。
- 基本的には、隣り合う2つの層の内、入力側(左側)にある層のニューロンの出力が、出力側(右側)のニューロンの入力になる。隣り合わない層同士はつながらない。(あくまで基本で、例外は多数ある)
- 入力層または中間層のあるニューロンの出力は、次の層のすべてのニューロンの入力になる。 (これも例外は多数ある) ある層のすべてのニューロンが、別の層のすべてのニューロンとつながるため、全結合と呼ばれている。
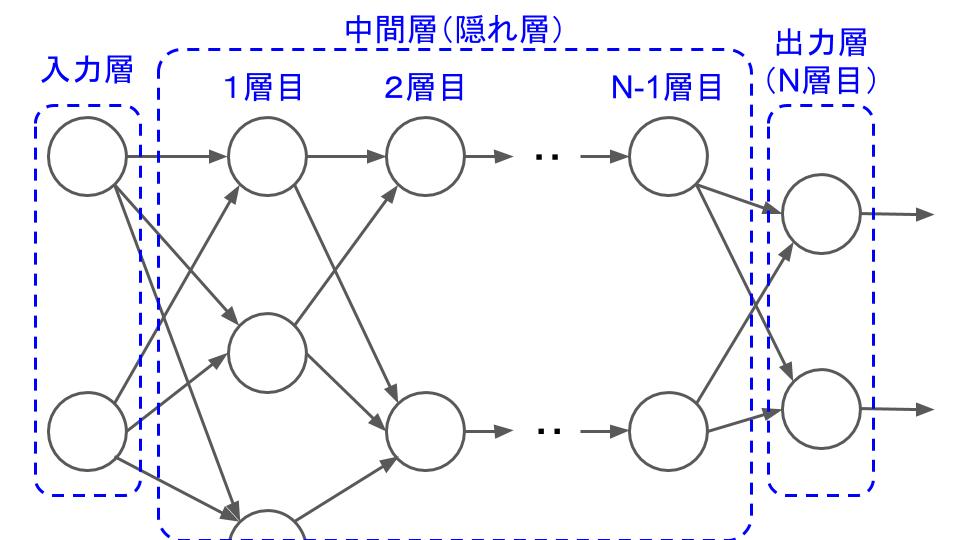
なので、実際に使う多層パーセプトロンはこんな感じに複雑なものになる。
中間層の数や各中間層のニューロンの数は、用途に応じて人間が決める必要があるけど、どれくらいにすれば計算が上手くいくのかについては、それだけで書籍が書き上がってしまうくらい議論が熱いところでもある。
この図にも書いているけど、「●●層の多層パーセプトロン」と呼んだとき、普通、入力層はカウントに入らない。中間層の最初の層から1層目、2層目、・・・と数えていき、出力層がN層目となったとき、「これはN層の多層パーセプトロンだ」となる。
特に、Nが4以上の深い層の多層パーセプトロンで機械学習を行う場合、私たちはディープラーニングと呼んでいる。
計算例
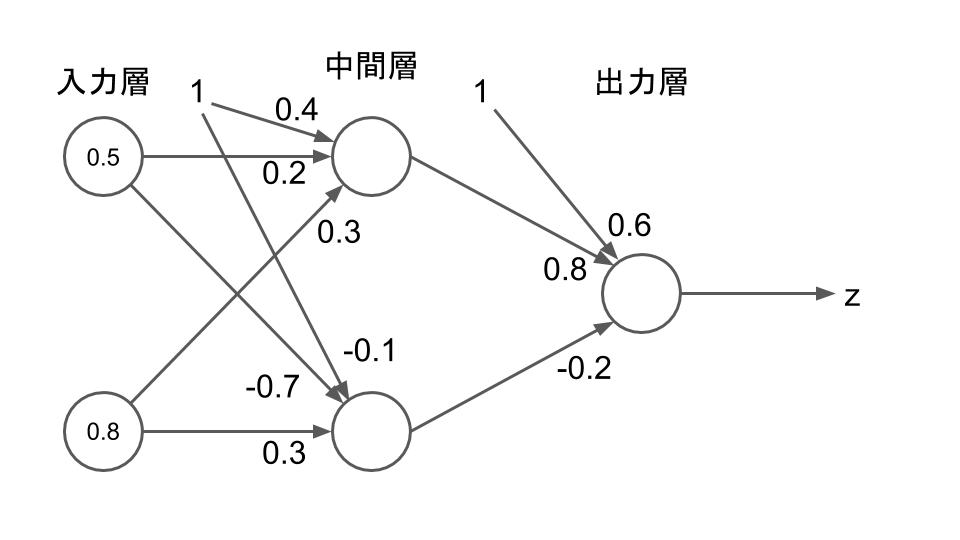
例えば、次の図のような入力、重み、バイアスを持つ2層のパーセプトロンを考えてみよう。
中間層のニューロンの付近にある0.4と-0.1はそれぞれのニューロンが持つバイアスで、出力層のニューロンの付近にある0.6は、出力層のニューロンが持つバイアスを意味する。
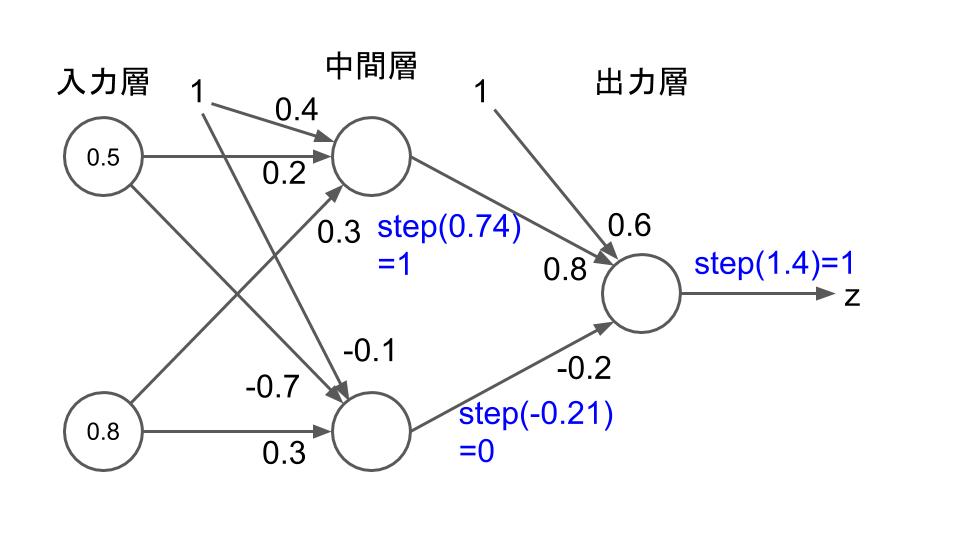
中間層・出力層のニューロンの活性化関数がステップ関数 \(\mathrm{step}\left(x\right)\) であるとすると、各ニューロンの出力は次のようになり、多層パーセプトロンの最終的な出力は1になる。
なぜパーセプトロンを多層にするだけで単体のパーセプトロンにはできなかった計算ができるようになるのか、については後日。