最小二乗法とは
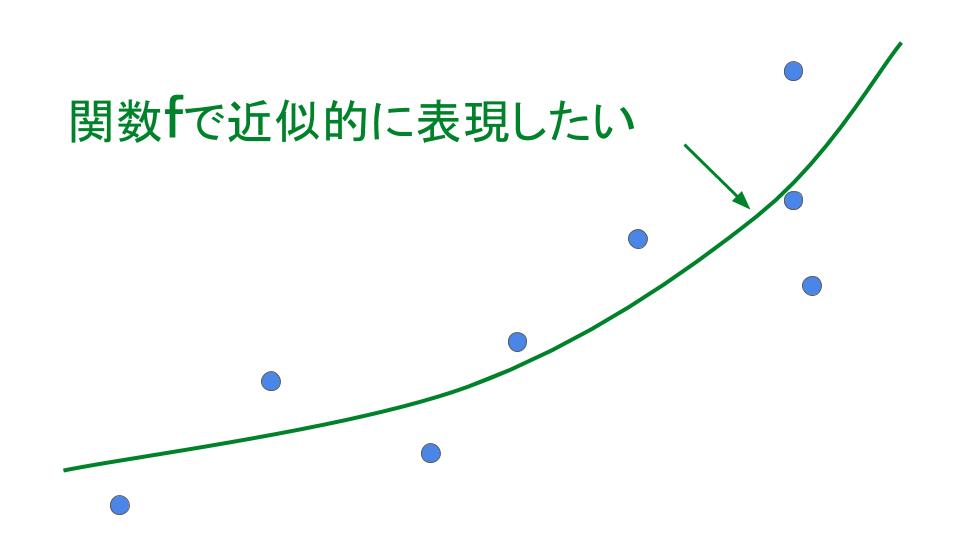
点の集合を関数 \(f\) で近似的に表現するにあたり,差の二乗和(後で説明する)が最も小さくなるように関数 \(f\) 内のパラメータを調整する方法。要するに下図のような感じ。
よくある誤解
たくさんの点 \(\left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right), \dots ,\left(x_{N},y_{N}\right)\) があって,それらとの誤差が最も少ない直線 \(y=ax+b\) をもとめるのが最小二乗法だ。という人がときどきいる。
これも,最小二乗法の一つの形だけど,これが最小二乗法のすべてではない。
直線でなくてもよい。2次関数でもよいし,3次関数でもよい。指数関数でもよいし,矩形波のような非線形関数でもよい。
2次元平面状でなくてもよい。3次元空間上でもよいし,4次元空間上でもよい。
差の二乗和とは
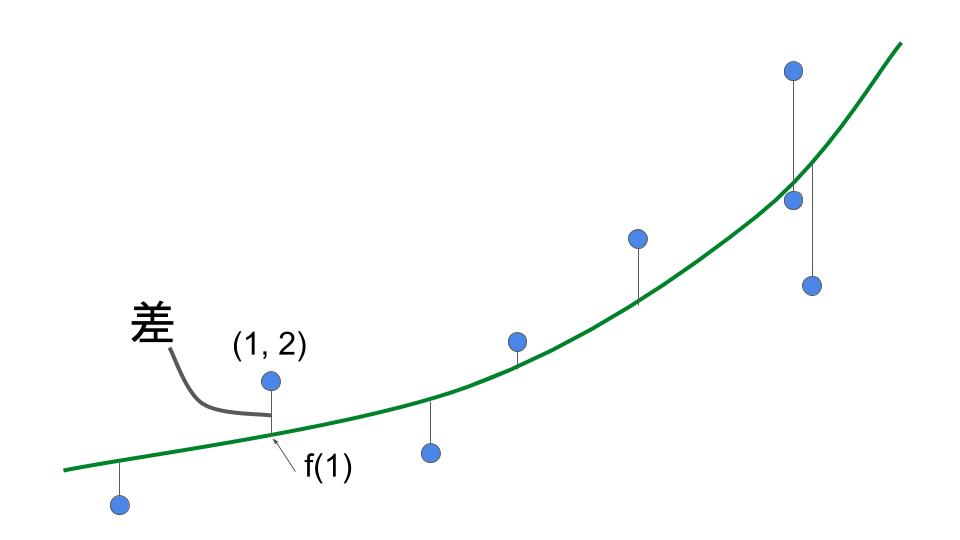
差は,各点と,関数値の差。
例1:点 \(\left(1,2\right)\) と関数値 \(f\left(1\right)\) の差
例2:点 \(\left(3.5,-6.8\right)\) と関数値 \(f\left(3.5\right)\) の差
例3:点 \(\left(2.3,3.4,5.6\right)\) と関数値 \(f\left(2.3,3.4\right)\) の差
差の二乗は,このような差を二乗したもの。
差の二乗和は,すべての点で計算した差の二乗を足し合わせてもとめた1つの値。
数式で書いてみよう。
\(M\) 次元空間に \(N\) 個の点と関数 \(f\) があり, \(N\) 個の点の座標が次の通りであったとする。
$$1点目:\left(x_{1,1},x_{1,2}, \dots ,x_{1,M-1},y_{1}\right),\\
2点目:\left(x_{2,1},x_{2,2}, \dots ,x_{2,M-1},y_{2}\right),\\
\dots\\
N点目:\left(x_{N,1},x_{N,2}, \dots ,x_{N,M-1},y_{N}\right)$$
このとき,すべての点と \(f\) との間の差の二乗和 \(E\) は次のように表現できる。
$$E=\sum_{i=1}^{N}\left[y_{i}-f\left(x_{i,1},x_{i,2}, \dots ,x_{i,M-1}\right)\right]^{2}$$
簡単な例
よくある,2次元平面状で直線に近似する場合について,差の二乗和がどう表現できるのか見てみよう。
2次元平面だから, \(M=2\)
直線に近似したいから, \(f(x)=ax+b\)
このとき,差の二乗和 \(E\) は次のように書ける。
$$E=\sum_{i=1}^{N}\left[y_{i}-\left(ax_{i,1}+b\right)\right]^{2}$$
\(M=2\) なので,簡単のため \(x\) の添え字は一部省略して次のように書こう。
$$E=\sum_{i=1}^{N}\left[y_{i}-\left(ax_{i}+b\right)\right]^{2}$$
\(E\) は任意の実数 \(a\) , \(b\) のいずれでも微分可能なので,Eが最小(極小)となるときは次の2つの式が成り立つ。
$$\frac{\partial E}{\partial a}=0\\
\frac{\partial E}{\partial b}=0$$
簡単な例を解いてみる
先ほどの式を解いてみる。
$$\frac{\partial E}{\partial a}=0\\
\Longleftrightarrow \frac{\partial}{\partial a} \sum_{i=1}^{N}\left[y_{i}-\left(ax_{i}+b\right)\right]^{2}=0\\
\Longleftrightarrow 2\sum_{i=1}^{N}\left[y_{i}-\left(ax_{i}+b\right)\right] \cdot \frac{\partial}{\partial a} \left[y_{i}-\left(ax_{i}+b\right)\right]=0\\
\Longleftrightarrow \sum_{i=1}^{N} \left[y_{i}-\left(ax_{i}+b\right)\right] \cdot x_{i}=0\\
\Longleftrightarrow a\sum_{i=1}^{N}x_{i}^{2}+b\sum_{i=1}^{N}x_{i}=\sum_{i=1}^{N}x_{i}y_{i}$$
$$\frac{\partial E}{\partial b}=0\\
\Longleftrightarrow \frac{\partial}{\partial b} \sum_{i=1}^{N}\left[y_{i}-\left(ax_{i}+b\right)\right]^{2}=0\\
\Longleftrightarrow 2\sum_{i=1}^{N}\left[y_{i}-\left(ax_{i}+b\right)\right] \cdot \frac{\partial}{\partial b} \left[y_{i}-\left(ax_{i}+b\right)\right]=0\\
\Longleftrightarrow \sum_{i=1}^{N} \left[y_{i}-\left(ax_{i}+b\right)\right]=0\\
\Longleftrightarrow a\sum_{i=1}^{N}x_{i}+Nb=\sum_{i=1}^{N}y_{i}$$
上の2式をまとめると次のような行列演算(連立方程式)で表現できる。
$$\begin{pmatrix}
{\displaystyle \sum_{i=1}^{N}x_{i}^{2}} & {\displaystyle \sum_{i=1}^{N}x_{i}}\\
{\displaystyle \sum_{i=1}^{N}x_{i}} & N\\
\end{pmatrix}
\begin{pmatrix}
\\
a \\
\\
b \\
\\
\end{pmatrix}
=\begin{pmatrix}
{\displaystyle \sum_{i=1}^{N}x_{i}y_{i}} \\
{\displaystyle \sum_{i=1}^{N}y_{i}} \\
\end{pmatrix}$$
後は,地道に吐き出し法などで手計算で解いてもいいんだけど,行列演算を行うプログラミング環境などがある場合は,そちらを使った方が効率よく \(a\) と \(b\) の値 が得られる。
行列内の各要素はかなり単純な \(\sum\) 演算なので,プログラミングの手間もそんなにかけずに各要素が数値として計算できる。
そこからは逆行列の計算をプログラムに任せれば \(a\) と \(b\) の値が得られるはずだ。
直線以外で最小二乗法がしたい場合
今回取り上げた簡単な例では,2次元平面上で直線を近似する場合について説明したが,最小二乗法は2次元以外でも,直線以外でも適用できる。
例えば,3次元空間内で滑らかな(微分できる)曲面の関数 \(f\left(x,y\right)\) で近似する場合にも同様の手順でできる。
3次元空間なので \(M=3\) である。
曲面の関数の形を \(f\left(x,y\right)=ax^{2}+by^{2}+cx+dy+e\) と仮定すると,差の二乗和 \(E\) は次のようになる。
$$E=\sum_{i=1}^{N}\left[y_{i}-\left(ax^{2}+by^{2}+cx+dy+e\right)\right]^{2}$$
\(E\) は \(a\) ~ \(e\) いずれでも微分できるので,差の二乗和を最小にするパラメータ \(a\) ~ \(e\) は次の連立方程式を解くと得られる。
$$\frac{\partial E}{\partial a}=0\\
\frac{\partial E}{\partial b}=0\\
\frac{\partial E}{\partial c}=0\\
\frac{\partial E}{\partial d}=0\\
\frac{\partial E}{\partial e}=0$$
Post Views: 5,605
関連