複数のニューロンから構成される最も基本的なネットワークはパーセプトロンと呼ばれている。たとえばこんな形をしている。(いつかのニューロンを解説した記事の図と似ているけれど、○はニューロン1つを表している。)
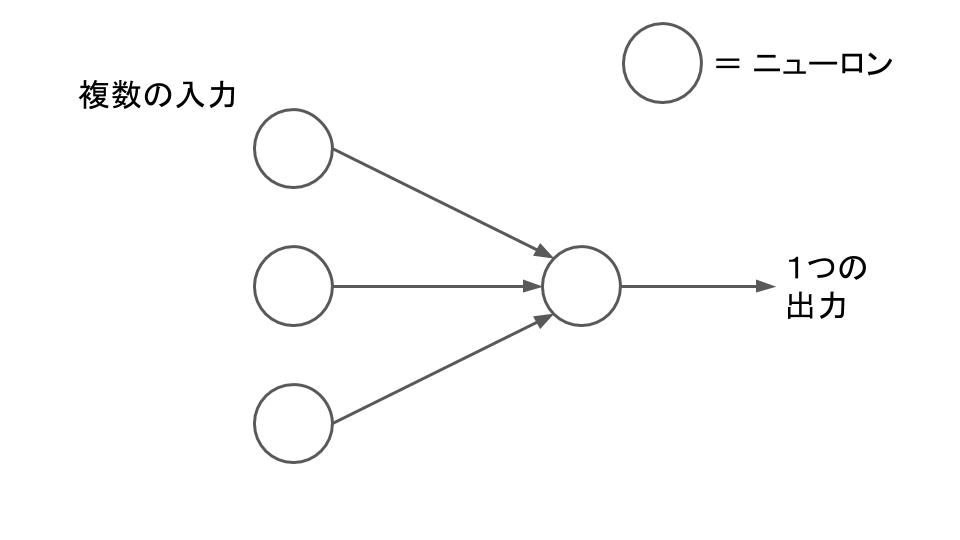
複数の入力をそれぞれ1個ずつのニューロンで受け取り、1つのニューロンから出力する。入力にニューロンが複数並んでいるけれど、これらは中で特に演算は行わず、そのまま出力側のニューロンに入力信号を渡す役割しか持っていない。あまり気にしなくてOK。ニューロン内部で演算するのは出力側にある1個だけ。
こんな単純なものでも、きちんと分類問題などがこなせる。例えば、入力が2つのパーセプトロンを考えてみる。こんなの↓
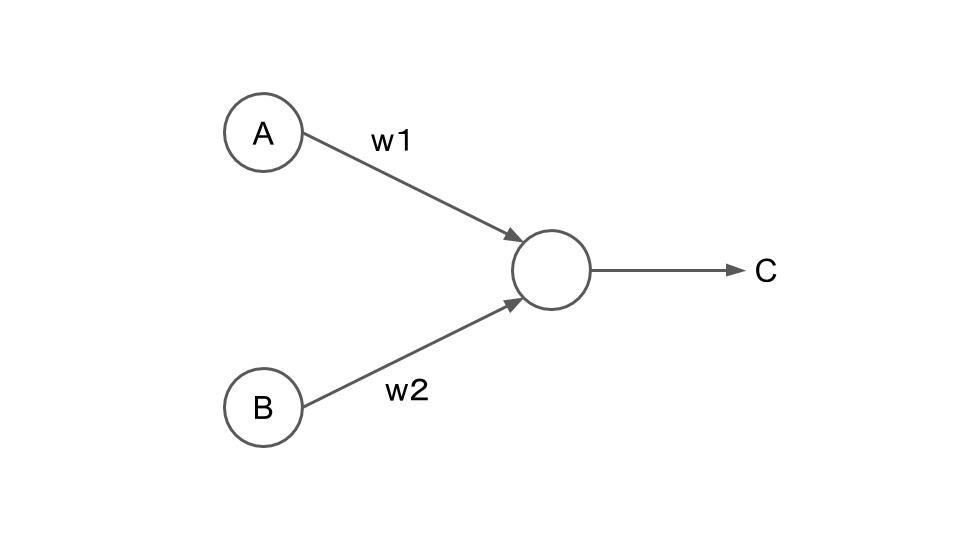
\(A\)と\(B\)は入力信号(0~1)、
\(w_{1}\)と\(w_{2}\)は出力側ニューロンに入力された信号(\(A\)と\(B\))に対してそれぞれ掛け算する数(「重み」という)、
\(C\)は出力信号(0か1のどちらか)である。
問題を単純にするために、ニューロンの活性化関数をステップ関数として考えてみよう。
ステップ関数を \(\mathrm{step}(x)\) で表すと、出力 \(C\) は次の式で計算できる。
$$C=\mathrm{step}(w_{1}A\cdot+w_{2}B\cdot+b)$$図には載っていなかった\(b\)というのは、出力側のニューロンが持つバイアスのこと。\(b\)が大きいと出力\(C\)は1になりやすく、逆に小さいと0になりやすい。
$$w_{1}=0.6\\ w_{2}=0.7\\ b=-0.8$$のとき、パーセプトロンはこんな感じ。
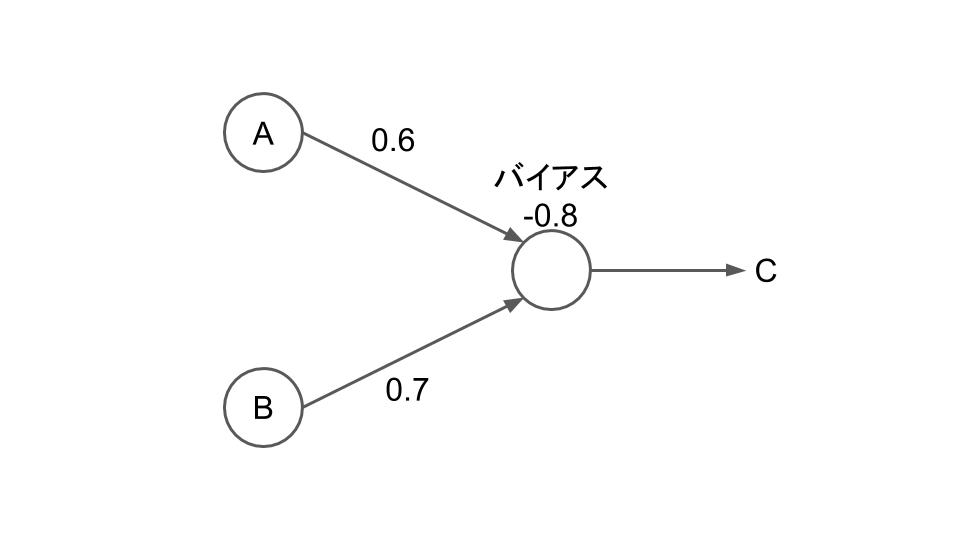
出力\(C\)はこうなる↓
$$C=\mathrm{step}(0.6A+0.7B-0.8)$$色々入力してみよう。
\(A=0.0, B=0.0\)のとき、\(C=\mathrm{step}(-0.8)=0.0\)
\(A=1.0, B=0.0\)のとき、\(C=\mathrm{step}(-0.2)=0.0\)
\(A=0.0, B=1.0\)のとき、\(C=\mathrm{step}(-0.1)=0.0\)
\(A=1.0, B=1.0\)のとき、\(C=\mathrm{step}(0.5)=1.0\)
お気づきだろうか。論理学や電子回路の基礎を勉強した人なら分かるかもしれない。これはAND回路になっている。
つまり、2つある入力が両方とも\(1\)のときにだけ出力が\(1\)となり、それ以外のときには\(0\)となる論理回路あるいはデジタル回路になっている。
これは、2つの入力が両方とも\(1\)のときはそれを\(1\)と分類し、それ以外の場合は\(0\)と分類する分類器ということもできる。
パーセプトロンの入力をもっと増やせば、もっと複雑なこともできる。もう立派な回路だ。
でも、パーセプトロンには意外と単純な限界がある。これについてはまた後日。
