
パーセプトロンにはどうしてもできない計算がある。今回はそれについて説明する。
ニューロンの活性化関数を\(f_{a}()\)で表現すると、例えば入力が2つ\(\left(x,y\right)\)あるパーセプトロンの出力\(z\)は次の式で表せる。計算の仕方についてはこちらを参照。
$$z=f_{a}(w_{1}x+w_{2}y+b)$$話を簡単にするために、活性化関数はステップ関数とする。このとき、出力\(z\)は次のように表現できる。
$$w_{1}x+w_{2}y+b>0のとき、z=1\\ それ以外のとき、z=0$$今からこれをもっと分かりやすい形に書き換えていく。
\(w_{2}>0\)と仮定すると次のように書き換えられる。
$$y>-\frac{w_{1}}{w_{2}}x-\frac{b}{w_{2}}のとき、z=1\\ それ以外のとき、z=0$$ここで、
$$\alpha=-\frac{w_{1}}{w_{2}}\\ \beta=-\frac{b}{w_{2}}$$とおくと、最終的にパーセプトロンの出力はこう表現できる。
$$y>\alpha x+\betaのとき、z=1\\ それ以外のとき、z=0$$これを図で表すと例えばこんな感じになる。(\(\alpha=1、\beta=1\)の場合)
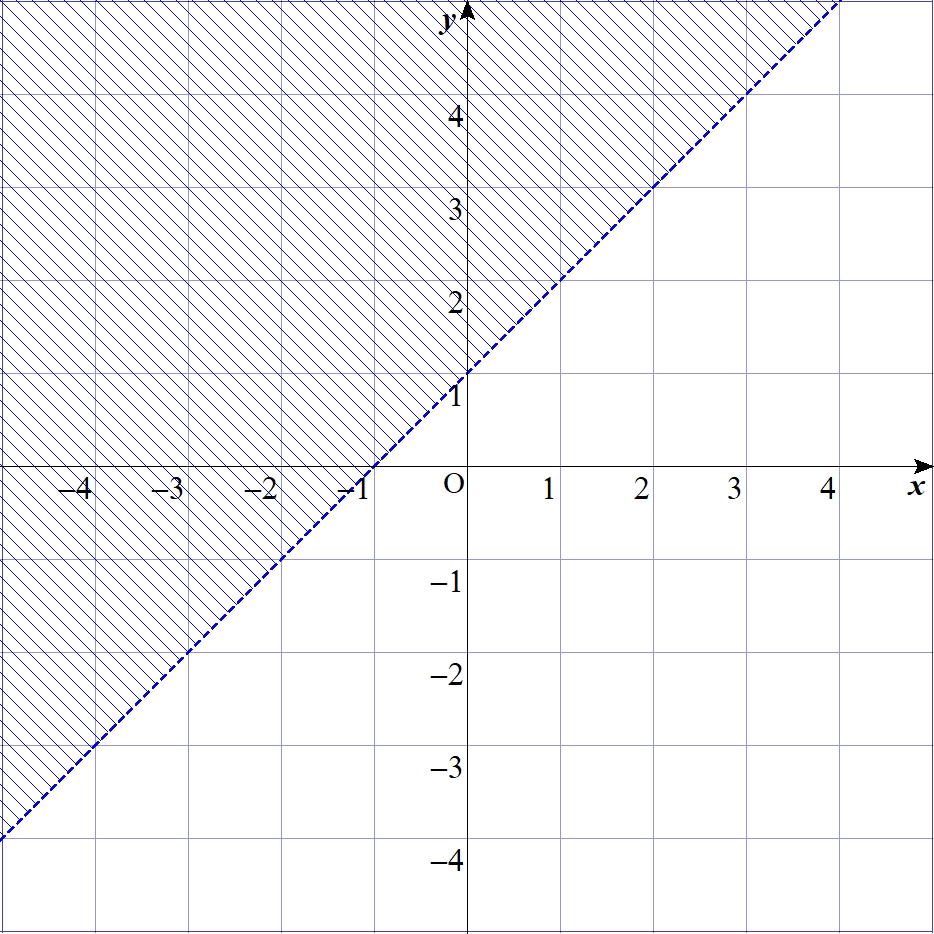
斜線で色が付けられた部分が\(z=1\)となる範囲で、それ以外の真っ白な部分が\(z=0\)となる範囲。
他にも、\(\alpha\)と\(\beta\)の値によって次のように変わる。
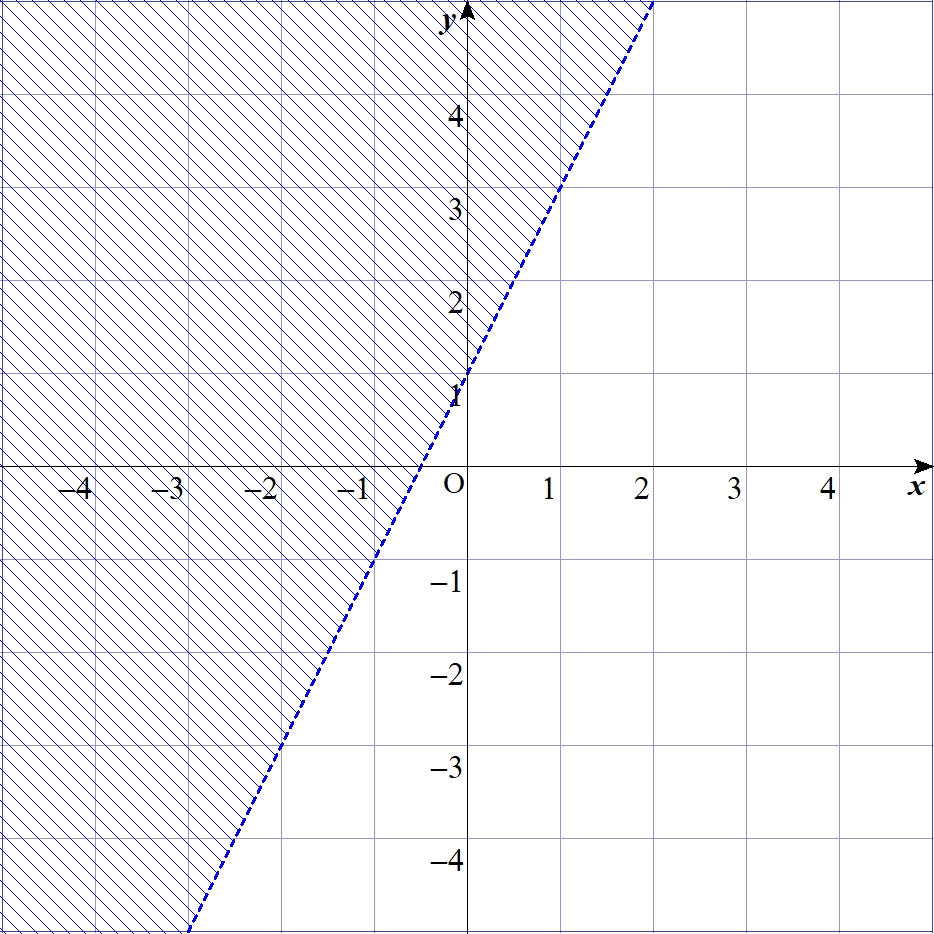
$$\alpha=2、\beta=1$$ 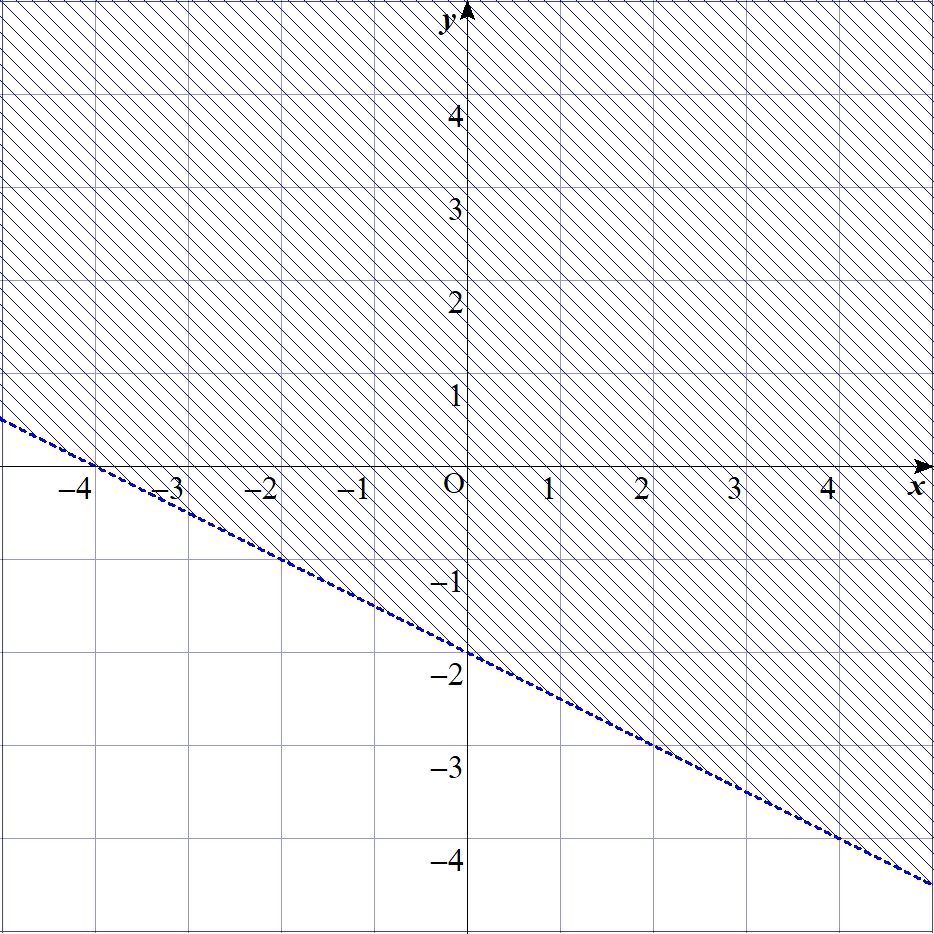
$$\alpha=-0.5、\beta=-2$$ 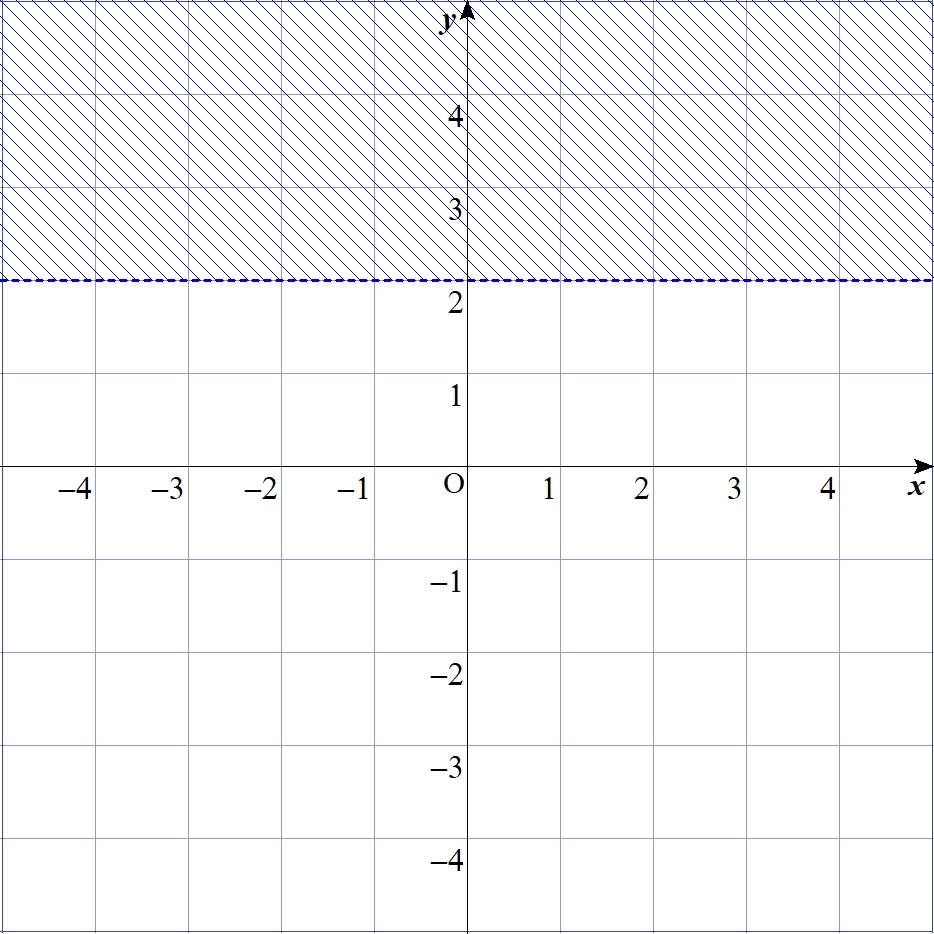
$$\alpha=0、\beta=2$$
さっきは\(w_{2}>0\)と仮定したけれど、\(w_{2}<0\)のときは数式の不等号が逆になるから、次のようになる。
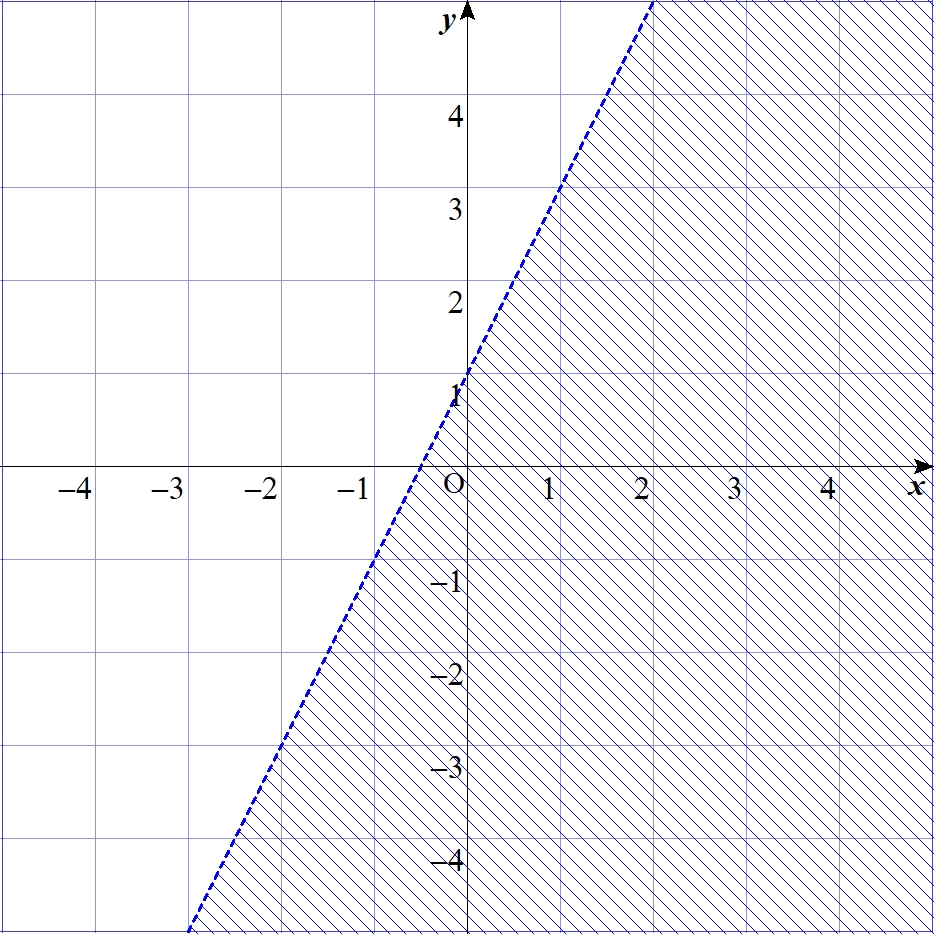
$$\alpha=2、\beta=1$$ 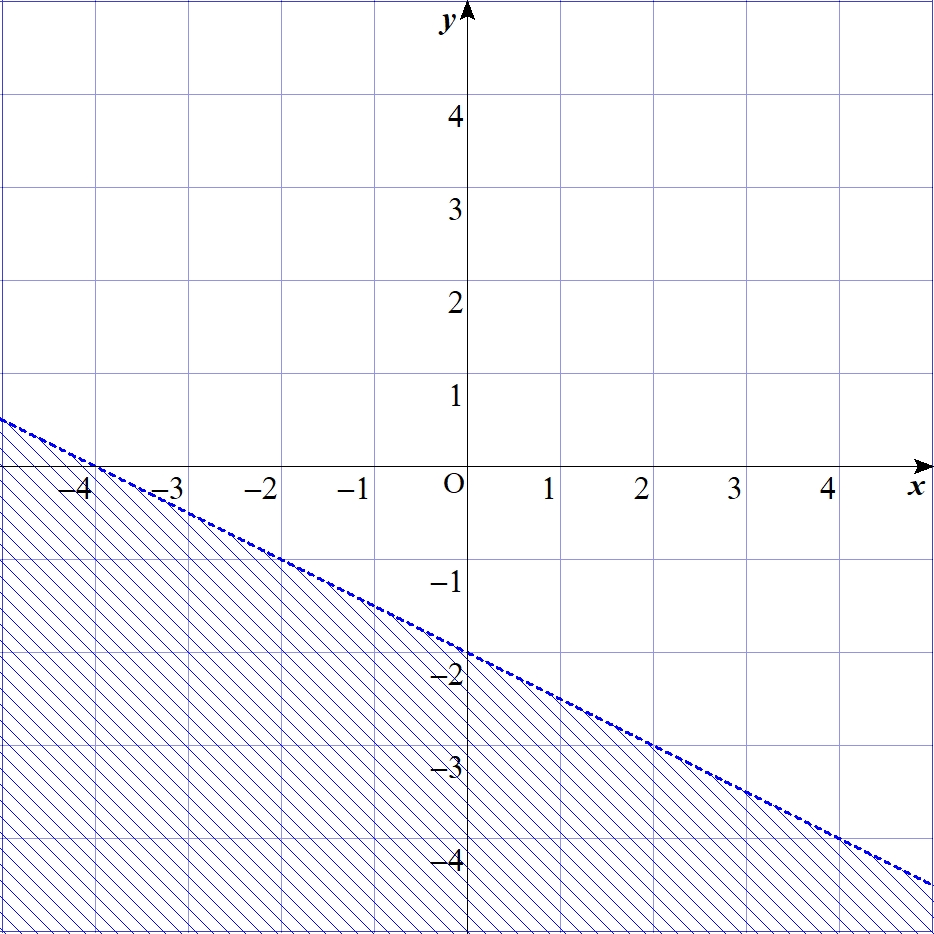
$$\alpha=-0.5、\beta=-2$$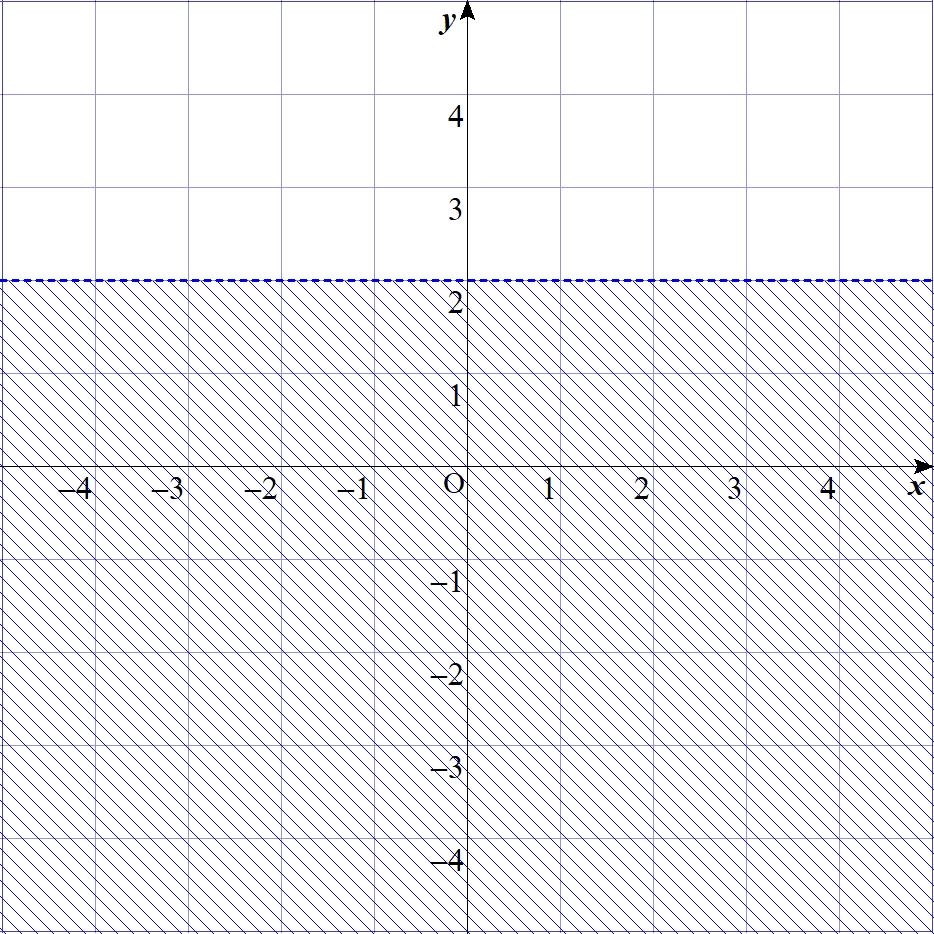
$$\alpha=0、\beta=2$$
このように、パーセプトロンでは\(z=1\)と\(z=0\)の境界がいつも直線になる。決して曲線や折れ線にはならない。(これは入力が3つに増えた場合にも境界がいつも平面になって似たようなことになる。)
例えば、入力\(x, y\)に対して次のように出力\(z\)が決められるようにパーセプトロンを作ろうと思っても、無理だということだ。
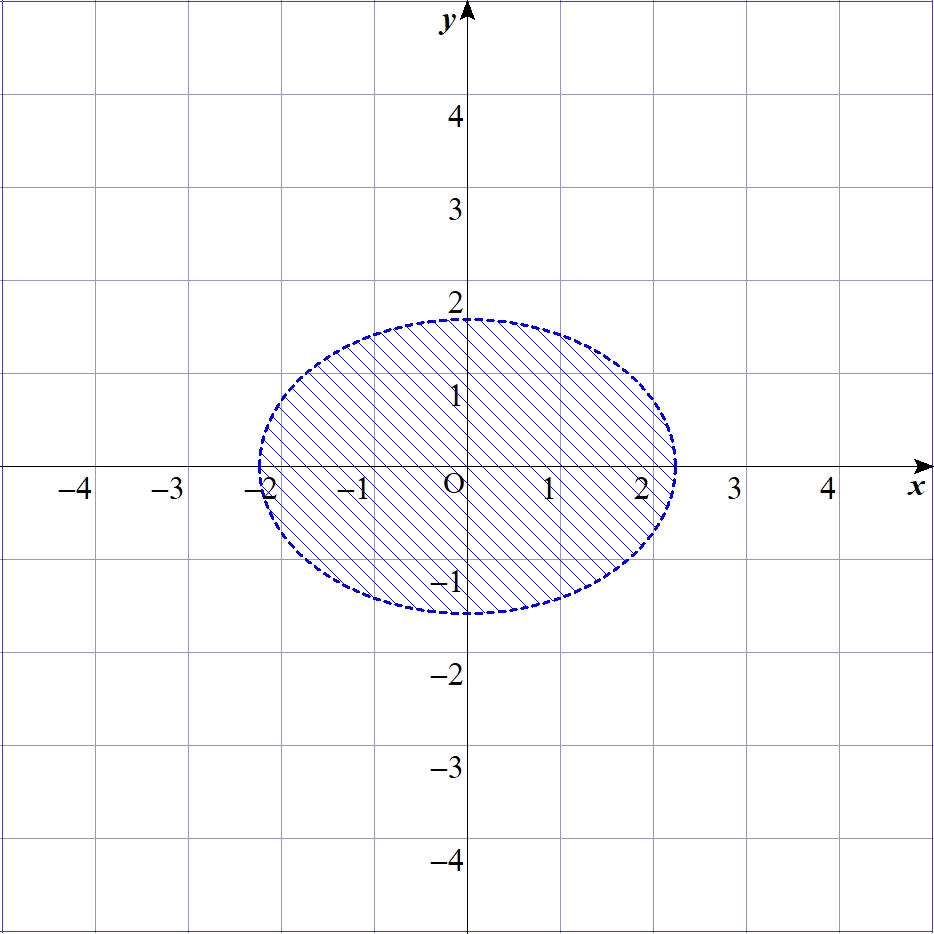
境界が閉じている 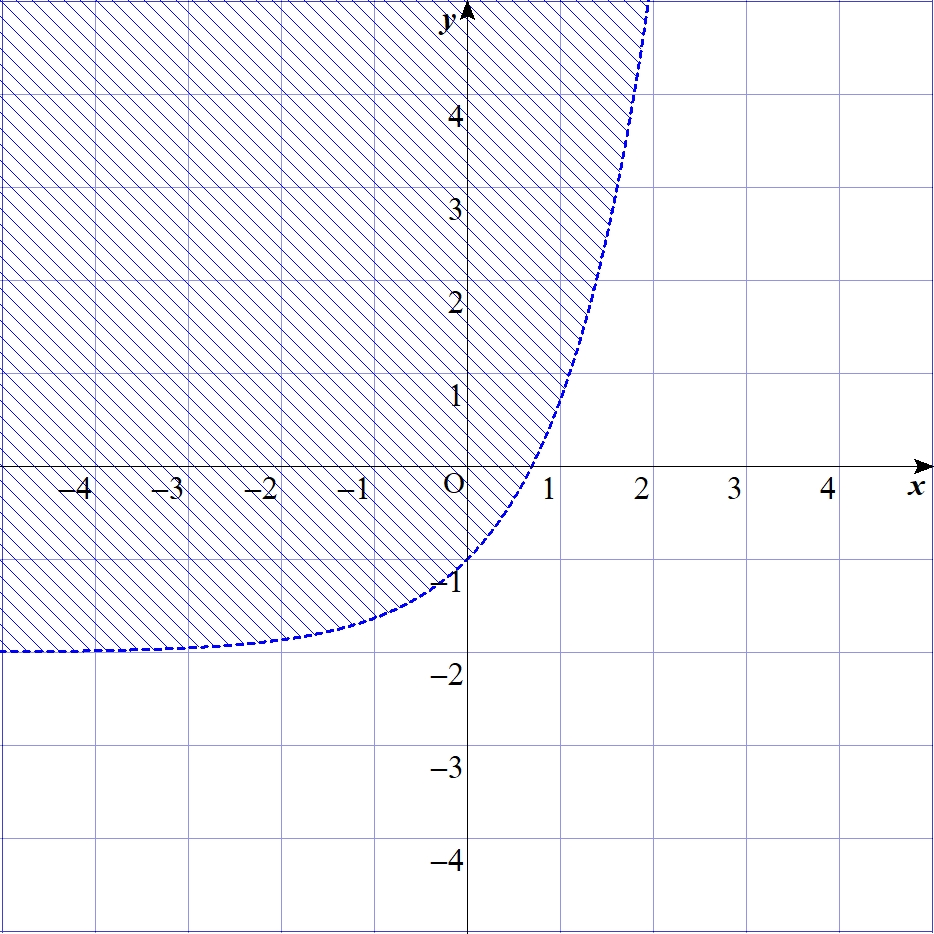
境界が曲がっている(または折れている) 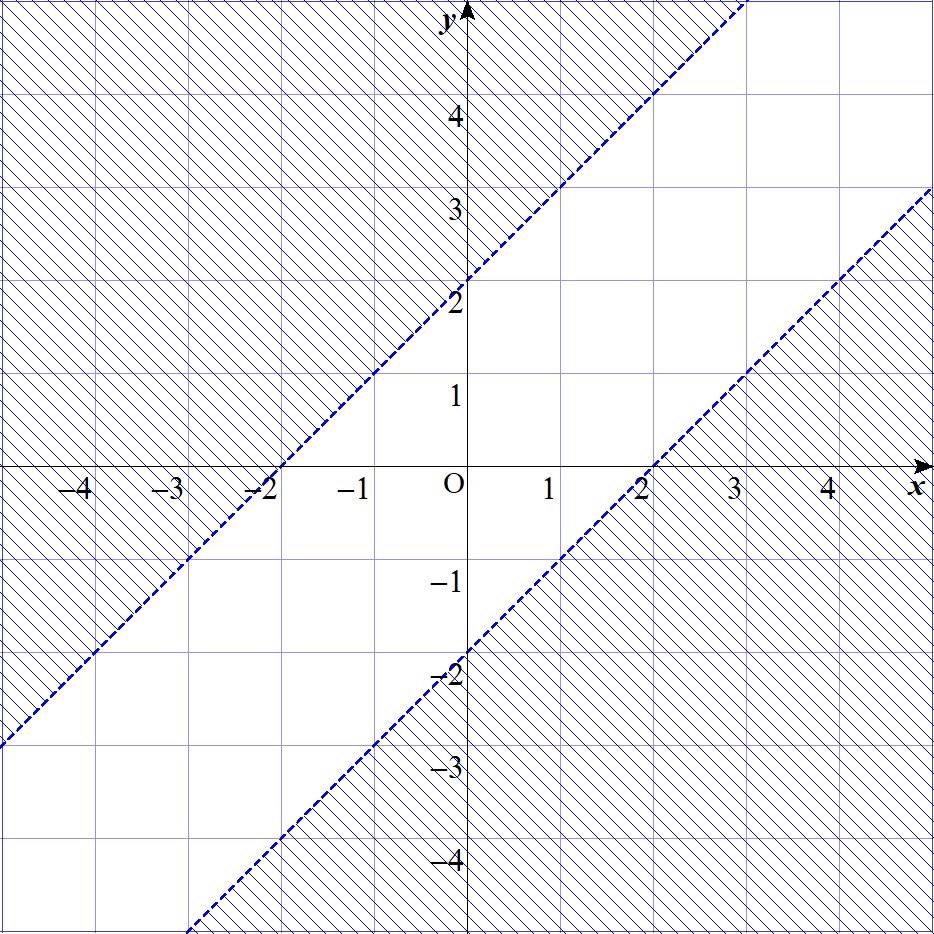
境界が複数ある
このため、複数の入力に対して少し複雑なことをしようと思ったら、パーセプトロンでは対応できない。
ディープラーニングなどのニューラルネットワークでは、この限界を克服するために、ニューロン同士をもっと複雑につないでいる。どうつないでどう計算しているのかについては後日。
